[AI_DeepLeaning_study CH02] 기울기 !야코비안 메트릭스! Backpropagation
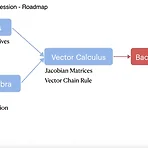
[선형회귀를 위한 수학 로드맵] 1. 미분 - 미분 계수 x가 변화할때 y의 변화량 도함수 : 기울기 ** 최적화 문제를 풀기위해 미분을 하는 이유는 업데이트 방향을 정해주기 위함. 예시) + 로가면 값이 더 커질거야 -로가면 값이 더 커질거야 도함수에 -를 붙인다면 값이 작아지는 방향을 알려줌 -4일때 +로가야 값이 작아짐 2일때 -로 가야 값이 작아짐 이것을 다항변수에 적용해보자 미분을 이용해 가장작은 점을 찾아보자. 칸토 ? 로그 스케일 :: 가운데로 optimal point 되는 과정 보기위해 로그 취해줌? gradients : 기울기 x증가량 분의 y증가량을 벡터로 편미분을 표현한것 그라디언트에 마이너스를 취해서 가장 작은 방향을 취한다. : 최적화 ! 차원을 좀더 높여서 .. 2. Jacobi..
AI
2023. 1. 25. 23:51
250x250
공지사항
최근에 올라온 글
최근에 달린 댓글
- Total
- Today
- Yesterday
링크
TAG
- three.js
- 유니티
- colab
- Unity
- opencv
- emotive eeg
- Express
- 라즈베리파이
- Java
- DeepLeaning
- Midjourney
- Arduino
- ardity
- CNC
- unity 360
- AI
- motor controll
- houdini
- imgtoimg
- RNN
- sequelize
- VR
- Python
- MQTT
- node.js
- 유니티플러그인
- 후디니
- oculuspro
- docker
- TouchDesigner
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
글 보관함
반응형